Solving the Schrödinger equation in one dimension
Here we give a simple Fortran code that calculates the eigenstates of the Schrödinger equation in one dimension, given a potential. The idea of the program is very simple: Potential and wavefunctions are discretized and the second derivative in the kinetic energy is approximated as a finite difference. Thus the Hamiltonian becomes a matrix, whose eigenvalues can be found using standard LAPACK routines. An explicit way of solving the eigenvalue problem would involve trial integrations of the Schroedinger equation and changing the trial energy until a state is found that has the proper boundary conditions. A very nice discussion of this procedure is given in the Feynman Lectures, Vol.3, Sec.16-6- Fortran code
- LAPACK routines (as downloaded from gams.nist.gov)
- BLAS routines (as downloaded from gams.nist.gov)
You can find the libarary routines also on GAMS: Search for module name dstevx
If on your system BLAS and LAPACK are installed, remove the last two lines in qm1d.f and link with your libraries instead.
To familiarize yourself with the code, have a look at qm1d.f and try to understand its structure:
- choose units and specify potential
- set up Hamiltonian
- call library routine to find eigenvalues and eigenfunctions
- prepare plot file

Here are some suggestions of what you could do:
- Run the code to get the ten lowest eigenstates for a particle in a box.
- Compare the numerical eigenenergies with the exact result.
- Change the width of the box (dx=width/dble(NPTS-1)). What happens?
- Why do the wavefunctions vanish at the boundaries? Look at the finite difference expression of the second derivative at the boundaries. What assumption has been made?
- Change the potential to a harmonic oscillator centered on the mesh.
- How should the spring constant be choosen? We want the nst
lowest eigenstates, and the mesh should be large enough that the
eigenfunctions have essentially decayed to zero on the boundaries.
Remember the exact result v(x)=(a*x)^2 ==> ee(n)=(2*n-1)*a
Thus for v(x) centered in the box, choose a such
that (a*width/2)^2 >> (2*nst-1)*a
example:dx=10d0/dble(NPTS-1) write(*,'("harmonic oscillator")') nst=10 do i=1,NPTS v(i)=4d0*(dble(i-1)-dble((NPTS-1)/2))**2*dx**2 enddo - Compare with exact solution. What happens when you
- increase/decrease the number of mesh points (try NPTS=51, 101, 201, 401)
- increase/decrease a on a fixed mesh (try a=2.0, 3.0, 4.0, 5.0 6.0)
- How should the spring constant be choosen? We want the nst
lowest eigenstates, and the mesh should be large enough that the
eigenfunctions have essentially decayed to zero on the boundaries.
Remember the exact result v(x)=(a*x)^2 ==> ee(n)=(2*n-1)*a
Thus for v(x) centered in the box, choose a such
that (a*width/2)^2 >> (2*nst-1)*a
- To improve the numerical accuracy, you could implement the Numerov method. But attention! The program as it stands assumes a symmetric Hamiltonian. So when implementing the Numerov method, you also have to use a more general diagonalization routine.
- For potentials with inversion symmetry the wavefunctions have parity.
For example: The ground state of the harmonic oscillator is symmetric with
respect to the center of the potential (even parity), while the first
excited state is antisymmetric (odd parity). It would be thus enough to
calculate the wavefunction on only one half of the potential.
- run the code for a harmonic potential centered on the left boundary of the mesh. What states do you find?
- States with even parity do not vanish at the center of the potential,
instead they have a vanishing first derivative. Change the boundary
conditions in the kinetic energy term such that you obtain the
even parity states (assume phi(-dx)=phi(dx)).
Unfortunately this makes the Hamiltonian matrix non-symmetric, so
we cannot use the simple diagonalization routine (which can only handle
tridiagonal symmetric matrices) here. A similar problem appears for
periodic boundary conditions. Then the Hamiltonian is no longer
tridiagonal.
In these cases, you have to use a general diagonalization routine. Something like that can be very easily implemented in systems like Matlab, Octave, IDL, or PV-WAVE. A brief PV-WAVE code looks, e.g., like
n=100 a=0.0005 H=dblarr(n+1,n+1) V=dblarr(n+1) for i=0,n do begin V(i)=a*double(i-n/2)^2 H(i,i)=2d0+V(i) if(i gt 0) then H(i,i-1)=-1d0 if(i lt n) then H(i,i+1)=-1d0 endfor ee=eig(H,vectors=ev,/symmetric) de=ee(n-1)-ee(n) plot, V, yrange=[0,ee(n-11)] for i=n-10,n do begin oplot, [1,n], [1,1]*ee(i) oplot, ee(i)+1.5*de*ev(*,i) endfor end
- Comparing with exactly known results is always an essential step
when working with numerical methods. It allows you to (i) check
if the code is correct and accurate and (ii) you make sure that
you really understand what the code is doing (choice of units,
influence of boundary conditions, etc.)
Now you are ready to go beyond exactly solvable cases
- Try the anharmonic oscillator
- v(x)=a1*x+a2*x^2+a3*x^3. The shifted harmonic oscillator can
be solved exactly; the x^3 term gives a good model for
the anharmonicity of molecular vibrations
(see, e.g., C.Cohen-Tannoudji, B.Diu, F.Laloe: Quantum Mechanics,
Vol.2, Complement A.XI)
To study molecular vibrations you can also use the Morse potential
![V(r)=D_e\left[\left(1-e^{-\beta(r-r_e)}\right)^2 -1\right]](./morseV.gif)
which, btw, is exactly solvable using supersymmetric quantum mechanics and has eigenenergies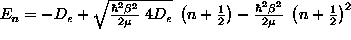
For a very brief introduction to supersymmetric quantum mechanics, see E. Koch: Superschalen in Metallclustern, Sec. 1.2 - v(x)=a2*x^2+a4*x^4, a4>0 For a2<0 you get a double well potential. Observe how, deep in the wells, you get pairs of states with very similar energy. What is the parity of the state with lower energy? (bonding/antibonding states).
- v(x)=a1*x+a2*x^2+a3*x^3. The shifted harmonic oscillator can
be solved exactly; the x^3 term gives a good model for
the anharmonicity of molecular vibrations
(see, e.g., C.Cohen-Tannoudji, B.Diu, F.Laloe: Quantum Mechanics,
Vol.2, Complement A.XI)
- Try a sinusoidal potential with 2, 3, 4, ... periods on the mesh (increase NPTS as required!) and observe groups of eigenstates. What would you get for a potential with very many periods on the mesh? (you can also try a finite Kramers-Kronig model)
- More things to try: lateral potential for 2-dim electron gas; use wavefunctions to calculate matrix elements
back
Erik Koch